by Ivan Iriarte MD, Simon Phoenix PhD
The recent controversy about vaccines approved for emergency use against COVID-19 has elicited much discussion regarding Relative Risk Reduction (RRR) and Absolute Risk Reduction (ARR). In broad terms, the ARR compares the overall outcomes of one event versus another; how much is the overall probability of an outcome reduced or increased? The RRR ignores overall improvement—it just compares the benefit, no matter how small, of one event versus another.
Relative to what?
Although we’re focusing on risk here, it’s worth noting the use (and misuse) of relative and absolute measures applies to many medical and scientific results. We must be careful not to rely purely on a relative measure, particularly if this relative measure is used in a headline-grabbing way. Suppose, for example, we have two cancer drugs, A and B. We are told that the tumour size reduction achieved by drug B was 100% better than that achieved by drug A. Drug B sounds very effective, doesn’t it? However, let’s suppose that in absolute terms drug A reduces the size of the tumour by 0.1% which would mean that drug B reduces the tumour by 0.2%. Neither drug could be said to be very effective in overall or absolute terms, but drug B is certainly more effective than drug A in relative terms.
Should you wear a rubber suit?
It’s often helpful to consider extreme examples when understanding technical ideas. Let’s imagine the invention of a rubberized, hooded suit that is designed to keep the wearer safe against lightning. It is found that the suit cuts lightning deaths so that for every 100 deaths by lightning in non-suit wearers there is only one death in suit wearers. This is an example of a high relative risk reduction (RRR). The absolute risk reduction (ARR) will be very small, however, because lightning strikes on people are very rare. In other words, wearing the suit changes an extremely small risk into an even smaller risk.
The real question is whether it is useful for everyone to wear rubberized suits to protect themselves from lightning? One might expect that most of us would probably answer “no”, even though the suits are very effective at preventing death from lightning. That assumes however no coercion, propaganda, or irrational fear influences the decision – a poor assumption in the era of COVID. Still, there may be occupations, such as communication tower maintenance, where wearing the suit would be sensible.
Thus, the ARR is an important consideration when trying to answer the question of whether something is worth doing. We might even argue that the ARR is a vital consideration, particularly in issues of societal impact.
In addition to understanding the definitions and meanings of ARR and RRR, it is important to understand how they should and should not be used. Although these concepts have acquired notoriety in the context of the COVID-19 immunizations, they have been used for decades as standard indicators to measure the efficacy of any preventive intervention.
For example, they are used to screen for the early detection of prostate cancer to help prevent death. Consequently, studies have been designed to compare the risk of death in individuals who receive screening compared to those who do not.
Does a randomized controlled trial always produce useful results?
These kinds of studies are usually randomized controlled trials (RCTs), generally considered the gold standard in validating the effect of any medical intervention. With a RCT, the investigators are able to avoid many of the limitations and biases that are likely to occur with other research methods. However, results from a RCT are not problem-free and should be interpreted with caution. Here once again the implications of RRR and ARR must be understood.
Typically, in a RCT, investigators will select subjects with specific criteria, and randomly assign them to one of two groups, the intervention group and the control or comparison group. Usually, the comparison group receives a placebo, which is an inert substance with no biological effect such as saline solution or sugar pill, and the intervention group receives the intervention being studied. Both the subjects and the investigators are blinded from knowing who is receiving the real intervention, eliminating a potential bias in the observations and reporting of data.
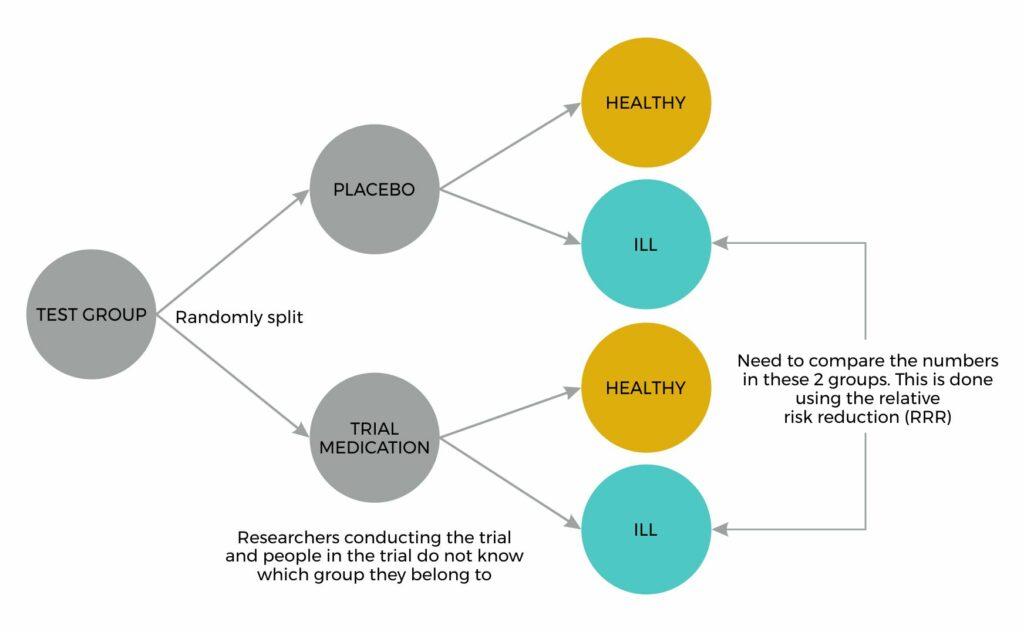
Figure 1: the basic structure of a RCT in which participants are either given the trial medication or a placebo. The numbers of people who become ill can be compared in the two groups and a relative risk reduction is estimated. Note that the test group must be split randomly so that each treatment group is truly comparable. Many studies fail at this basic step because the treatment groups are biased, and not truly equivalent populations.
The Pfizer Vaccine trial: designed for success not value?
The RCT method was applied to the Pfizer-BioNTech vaccine trials. The investigators randomly assigned 21,720 subjects 16 years and older to receive two doses of the new vaccine, and 21,728 subjects to receive two doses of placebo. They followed the subjects for a median of two months after the intervention.
It is also important to take into account the trial design itself. In this case Pfizer designed the trial, and they are highly experienced in setting up trials for success. The trial compared the case numbers in the vaccinated vs control (placebo) groups where a case of COVID-19 was defined as an individual who experienced symptoms and had a positive test for SARS-CoV-2 infection. This is arguably a weak endpoint, as incidence of severe disease and death, the very outcomes one would hope the vaccine prevents, were not considered. Other data was collected, including the incidence of serious side effects.
The trial reported eight cases of COVID-19 (as defined above) among the immunized group and 162 in the placebo group. So, the risk of COVID-19 in the immunized group was 8/21,720 = 0.037%, and the risk in the unimmunized group was 162/21,728 = 0.745%. The ARR is defined simply as the difference in risk between the two groups. In this case it would be = 0.745% – 0.037% = 0.708%; we will round it to 0.7%. The RRR is the ARR expressed as a percentage of the absolute risk of disease in the unvaccinated. In this case, it is = 0.708/0.745 = 95%. This RRR is what is reported (this is standard practice) as the “efficacy” of the vaccine.
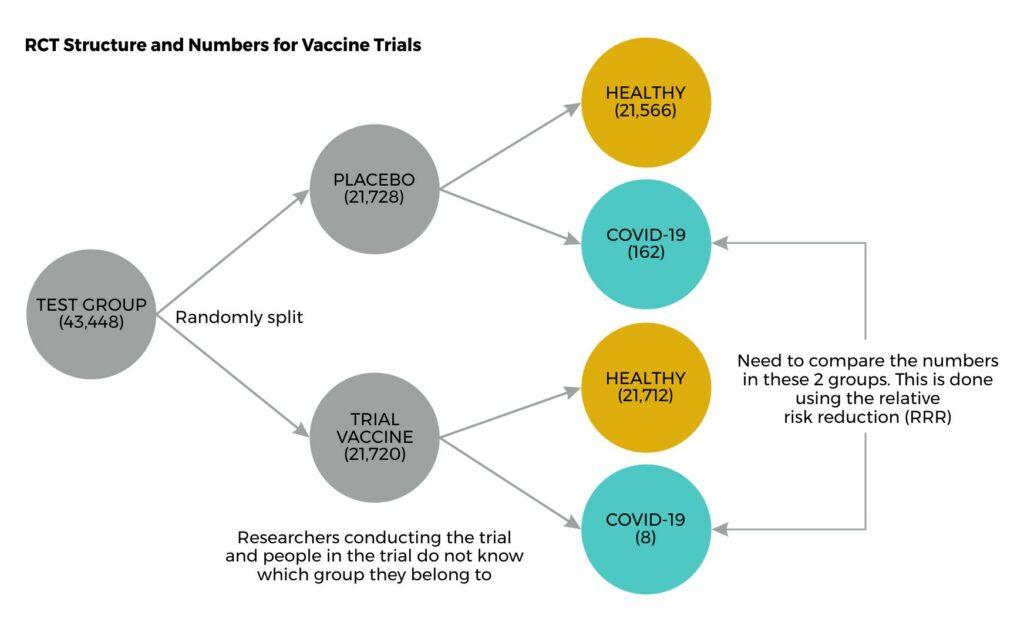
Figure 2: the basic structure of the vaccine RCT in which participants are either given the trial vaccine or a placebo. The numbers of people who experienced symptoms (and had a positive test) can be compared in the two groups and a relative risk reduction estimated.
It’s not that simple
The vaccine appeared to reduce the relative risk of COVID-19 (as defined by Pfizer) by an estimated 95% over the short duration of the trial, but the interpretation of that number is not that simple. It’s nearly impossible to extrapolate the potential real world benefit from such a limited trial design.
Firstly we must understand the role of statistics here. If you toss a coin 10 times you would expect to get 50% heads and 50% tails on average. In practice, however, it would not be too surprising to obtain 7 heads and 3 tails in any 10 tosses of the coin. There are similar considerations that apply to any medical trial. Although the headline figure here is a 95% relative risk reduction, how confident are we that this figure is close to the truth? If we had run the trial at another time, might we have only recorded a value of 90% for the RRR? So any quoted reduction must also come with some indication of how “good” that number is. While the Pfizer trail had 40000+ participants, relatively few were infected with COVID, leaving the conclusions to be based on small numbers.
In order to determine if the administration of the vaccine to the population is really beneficial, we also need to consider the actual risk of disease in those who did not receive the intervention. To illustrate with an exaggerated example, if the risk of acquiring a disease is only one in a million, reducing it by half, to one in 2 million is not a big deal. If, however, the risk of acquiring a disease is 30%, reducing the risk to 15% is very significant. If our proposed experimental treatment caused side effect deaths at a rate of one in a million we would be hesitant to recommend it in the above example, but we would be much more likely to recommend it for the latter.
The Pfizer study includes a figure that compares the cumulative number of vaccinated patients that became ill versus the cumulative number of placebo patients that became ill. The graph looks similar to this:
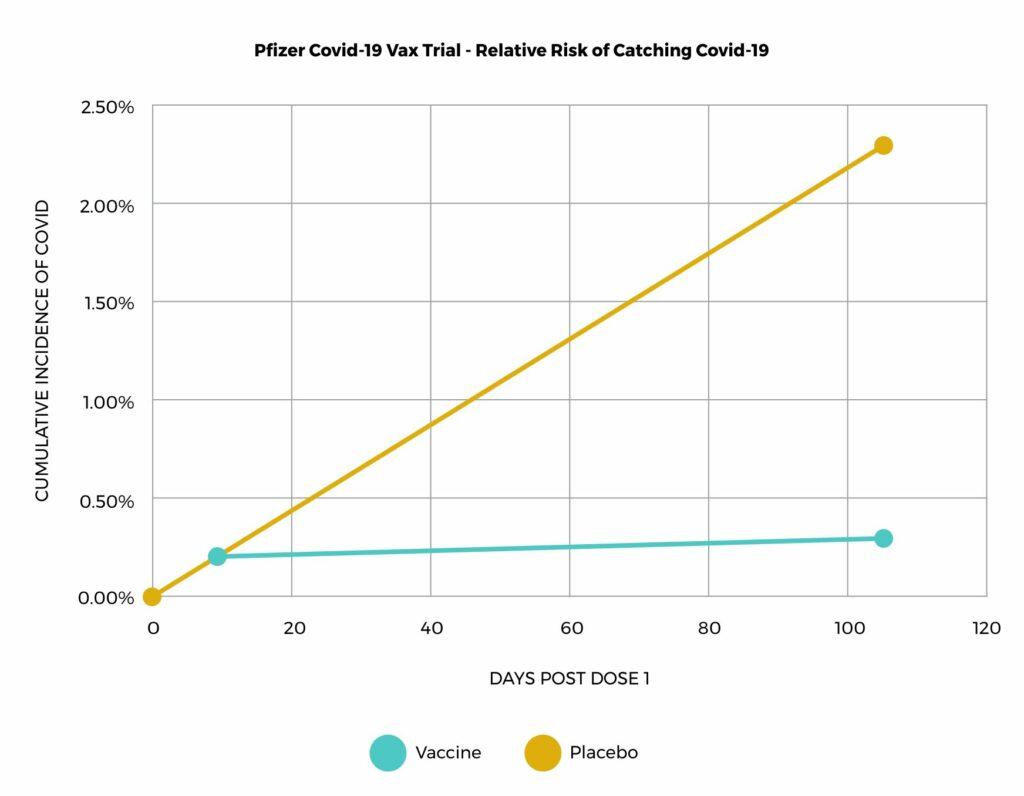
This appears to be an impressive result, as there are more cases in the placebo group RELATIVE to the vaccinated group. But note the Y axis only goes to 2.5% – so that in total 2.3% of placebo patients became ill versus .3% of vaccinated patients. If we look at the
ABSOLUTE RISK of each group, the results look far less impressive:
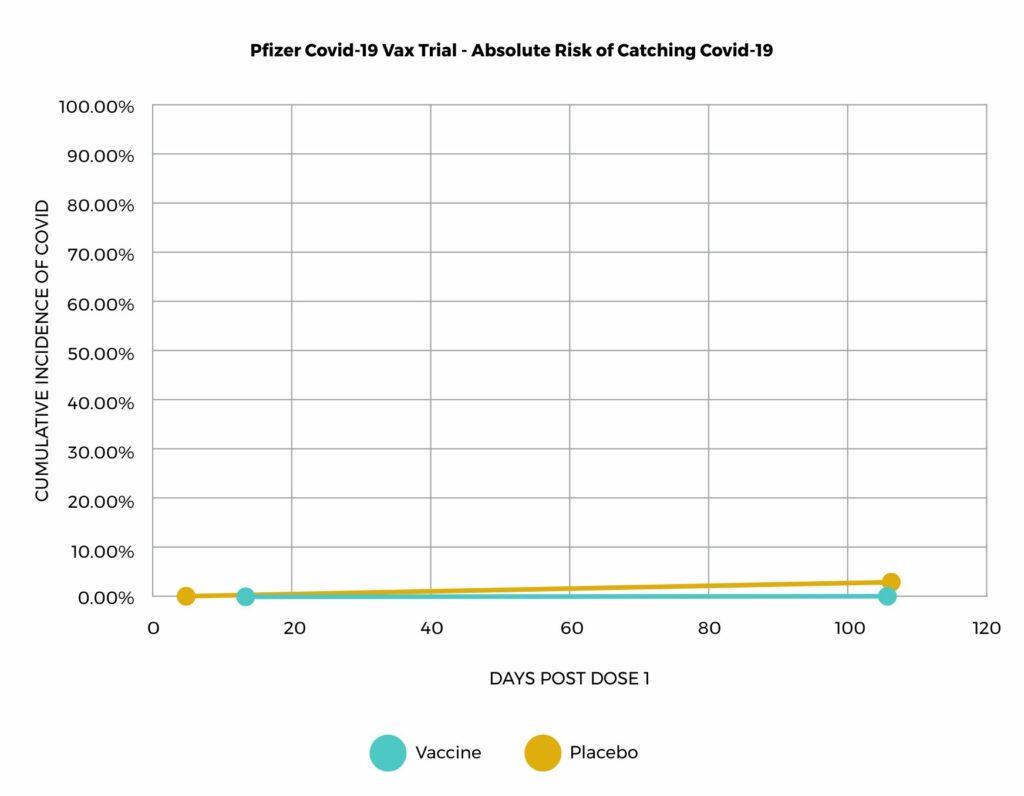
Is the benefit worth the cost?
This is the same question we asked in the rubberized lightning suit example above. It is the more difficult subjective question of whether our proposed measure is worth it. In the case of a serious disease like Covid19 this is a complex question because whilst we want to save lives, we also recognize that the vaccines, like all medical interventions, are not free from serious side effects. Even though only a small percentage suffer such effects, we must weigh this against the fact that we are also dealing with mostly small percentages of people (depending on personal risk factors) who die from COVID-19. The ARR and RRR are both important parameters that help us in addressing these complex issues
This illustrates why considering the ARR may be helpful. In the Pfizer clinical trial mentioned above, the risk of COVID-19 = 0.75%; so, reducing this risk by 95% does not seem like a very impressive effect. But the issue becomes even more complex to interpret. Within the clinical trial, different subgroups of people have different risks of getting COVID-19. Furthermore, different age groups have vastly differing risks of mortality from COVID-19. We cannot simply assume that a relative risk reduction of 95% applies uniformly across all age ranges from the trial data without further age stratification of the results. In general, younger people have massively lower risks from COVID-19, so the ARR is tiny in those groups. In addition, the risk of getting the disease in different sectors of the population, and in different geographical locations, may also be different.
There is a final important point to consider relative to trial design and reported outcomes. Whilst it is important to determine whether the vaccines are effective at reducing infection, it is equally important to know whether they improve health outcomes overall – is the benefit sufficient to justify the potential risk? For example, in the vaccine trial discussed above, there were 262 serious adverse events noted in the vaccinated group and 172 serious adverse events noted in the placebo group (which admittedly seems odd as one wouldn’t expect a saline injection to produce any adverse events). Given that, for the vast majority, COVID-19 is not a serious illness , adverse events arising during the trials should also factor into our decision about overall suitability of the proposed measure.
The logical conclusion is that the RRR and ARR of an intervention (in this case a vaccine) reported in a RCT should be interpreted carefully when making decisions about the desirability of implementing the intervention in the general population. It is not sound public health practice to say: “This vaccine is 95% effective, so let’s give it to everyone”. The decisions to implement interventions in the population should use results of a RCT as valuable information, but should also take into account many factors such as the actual risk of getting COVID-19 in different populations (geographical locations, different ages, other medical conditions…), the probability of getting sick with COVID-19 during different seasons, and the probability of adverse events following vaccination among others.
References:
1. Olifaro, P. et al. COVID-19 vaccine efficacy and effectiveness—the elephant (not) in the room. https://www.thelancet.com/journals/lanmic/article/PIIS2666-5247(21)00069-0/fulltext
2. Schröder FH, et al. Screening and prostate-cancer mortality in a randomized European study. N Engl J Med. 2009; 360:1320-8. https://www.nejm.org/doi/full/10.1056/nejmoa0810084
3. Pollack, FP. Et al. Safety and Efficacy of the BNT162b2 mRNA Covid-19 Vaccine. https://pubmed.ncbi.nlm.nih.gov/33301246/




